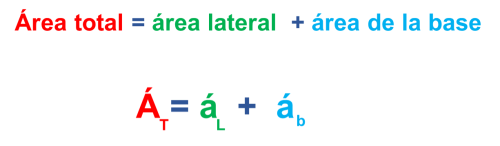sueperacion tercer periodo EJEMPLO 1: (Suma de polinomios de igual grado) A = - 3x2 + 2x4 - 8 - x3  + 1/2 x B = -5x4 - 10 + 3x + 7x3     2x4  -  x3  - 3x2 + 1/2 x  -  8         +    -5x4 + 7x3 + 0x2  +   3x  -  10         ______________________________    -3x4 + 6x3 - 3x2 + 7/2 x  - 18 A + B = -3x4 + 6x3 - 3x2 + 7/2 x  - 18 Para sumar dos polinomios, hay que sumar entre sí los coeficientes de los términos del mismo grado El resultado de sumar dos términos del mismo grado, es otro término del mismo grado. Si falta algún término de alguno de los grados, se puede completar con 0, como en el ejemplo en el segundo polinomio se completó con 0x2. Y se los suele ordenar de mayor a menor grado, para que en cada columna queden los términos de igual grado. También se los puede sumar de otra forma (sin ponerlos uno sobre otro), y en la EXPLICACIÓN de cada ejercicio lo mostraré resuelto de las dos maneras. EXPLICACIÓN DEL EJEMPLO 1  EJEMPLO 2: (Suma de polinomios de distinto grado) A = -3x2 + 5x - 4             B = 4x3 - 5x2 + 2x + 1         0x3 - 3x2 + 5x - 4         +    4x3  - 5x2 + 2x + 1       ____________________    4x3  - 8x2 + 7x - 3 A + B = 4x3  - 8x2 + 7x - 3 En el polinomio de menor grado, se pueden completar los primeros términos con ceros. Así, se rellenan las columnas que faltan adelante de uno de los polinomios, para que quede encolumnado término a término con el otro polinomio. EXPLICACIÓN DEL EJEMPLO 2

EJEMPLO 3: (Uno de los términos del resultado es cero) A = 9 + 5x3 - 4x2 + x B = 4x2 - 3 - 2x    5x3  - 4x2 + x + 9 +    0x3 + 4x2 - 2x - 3 ____________________    5x3 + 0x2 - x  + 6 A + B = 5x3 - x  + 6 La suma de los términos de grado 2 dió 0x2. Luego, en el resultado final ya no se ponen los términos con coeficiente cero. EXPLICACIÓN DEL EJEMPLO 3 EJEMPLO 4: (No hay términos semejantes) A = 4x3 + 5 B = -2x + x2    4x3 + 0x2 + 0x + 5 +    0x3 +  x2 - 2x + 0 ____________________    4x3 +  x2 - 2x + 5 A + B =  4x3 +  x2 - 2x + 5 Se llama términos "semejantes" a los que tienen el mismo grado (en los polinomios con un solo tipo de letra). Entre estos dos polinomios no hay términos semejantes. Se puede observar que el resultado es la suma de todos términos de los dos polinomios, sin modificarse ninguno, ya que a cada uno se le sumó cero, por no tener otro término semejante. EXPLICACIÓN DEL EJEMPLO 4 EJEMPLO 5: (Suma de polinomios de varias letras) A = -3xy2 + 4 - 7x2y2 - 6x2y - 5xy B = 8xy - 2xy2 + 10 + 4x3y A + B = (-3xy2 + 4 - 7x2y2 - 6x2y - 5xy) + (8xy - 2xy2 + 10 + 4x3y) = -3xy2 + 4 - 7x2y2 - 6x2y - 5xy + 8xy - 2xy2 + 10 + 4x3y = -3xy2 - 6x2y + 4 + 10 - 5xy + 8xy - 2xy2  + 4x3y  - 7x2y2 = -9xy2 + 14 + 3xy - 2xy2  + 4x3y - 7x2y2 Cuando los polinomios tienen varias letras, se suman los términos semejantes, que son los que tienen las mismas letras con los mismos exponentes (la misma"parte literal"). Para sumar estos polinomios, no es práctico usar el procedimiento de ordenarlos y sumarlos "en columnas", porque en general hay pocas coincidencias entre sus partes literales. Así que es mejor sumarlos "uno al lado del otro" y "juntar" los términos de igual parte literal.

ÁREA SUPERFICIAL Y VOLUMEN DE UNA PIRABIME

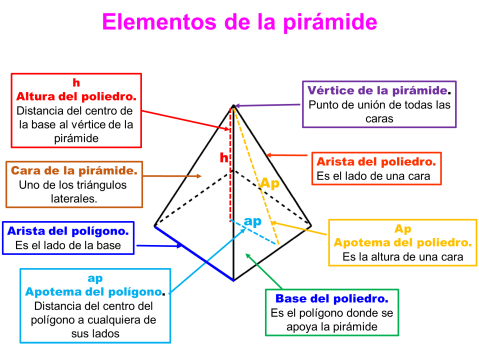
Pirámide es un poliedro cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice común llamado vértice de la pirámide.

Recordemos  los elementos de una pirámide

Para calcular el área total de una pirámide es necesario conocer:

1. El área de la base (áb ), que es el polígono donde se apoya la pirámide.
2. El perímetro de la base(pb ), que es la longitud de todas las caras.
3. La apotema de la base (ap), que es la distancia del centro de la base a cualquier lado.
4. La apotema de la pirámide (Ap), que es la altura de una cara lateral.
5. La altura del poliedro (h), que es la distancia que hay del centro de la base al vértice de la pirámide.

Si deseas el formulario para obtener el volumen haz clic aquí

Las fórmulas generales para obtener el área y el volumen de una pirámide son las siguientes:

Ejemplos de ejercicios de área y volumen de una pirámide.

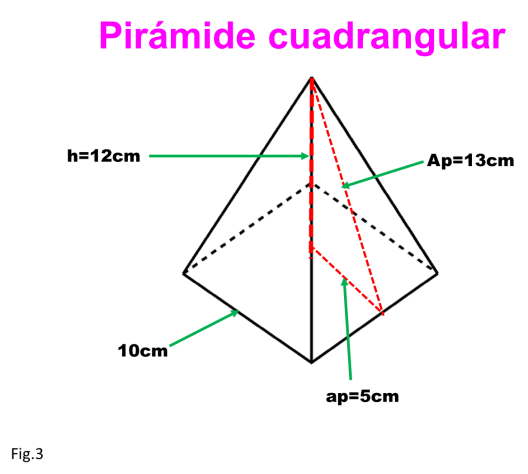
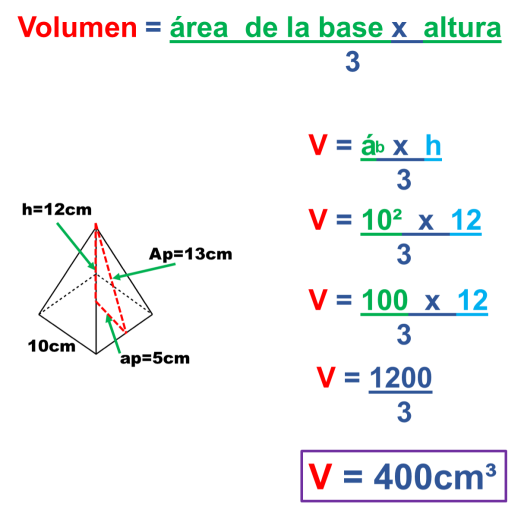
1.- Hallar el área total y el volumen de una pirámide cuadrangular cuya arista de la base mide 10, la altura de 12 cm y un Apotema del poliedro de 13 cm.

Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema

indica que es una pirámide cuadrangular con las siguientes medidas:

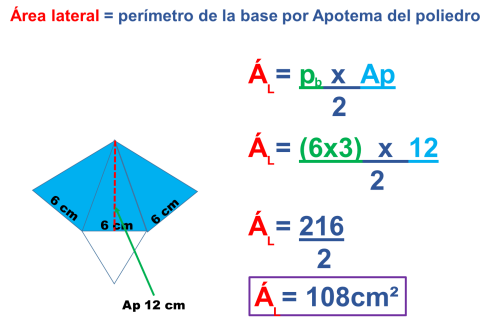
Obtengamos primero el área lateral (el de las cuatro caras triangulares) que es el área coloreada.

Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).

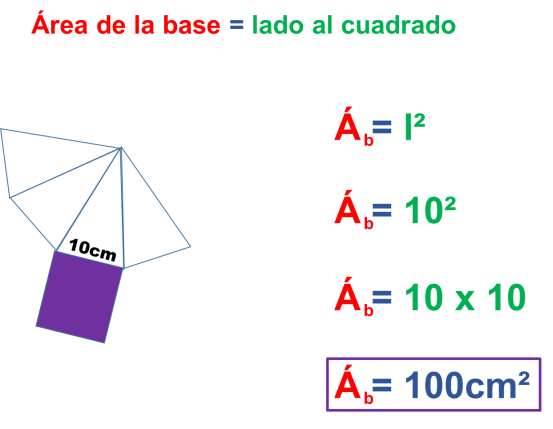
Y ahora el área de la base. Para ello en la fórmula general vamos  a sustituir por la fórmula para obtener el área de un cuadrado, ya que la base es cuadrangular.  Es el área coloreada.

Ver vídeo (Para recordar cómo se obtiene el área de un cuadrado).

Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide cuadrangular especificada.

Ahora obtenemos el volumen de la pirámide cuadrangular  sustituyendo la fórmula del área de la base por la del área del cuadrado y multiplicando por la altura del poliedro.

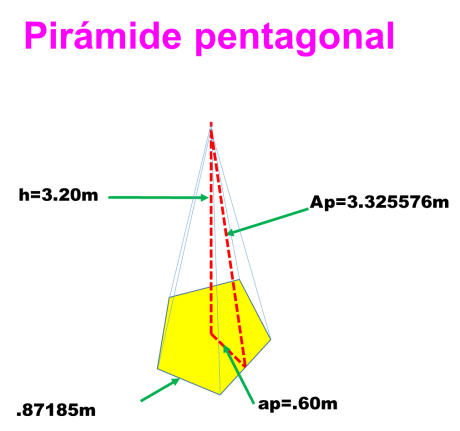
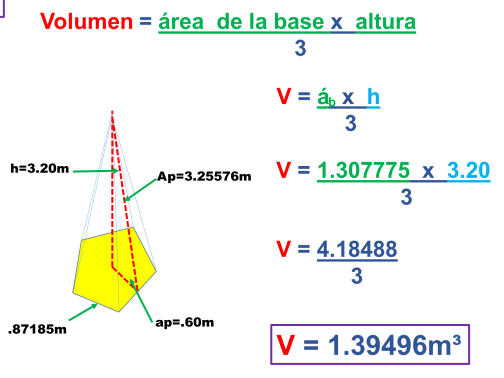
2.- Hallar el área total y el volumen de una pirámide regular pentagonal cuya altura mide 3.20m, el lado de la base 0.87185m, el apotema del poliedro 3.25576m;  y el apotema de la base 0.60m

Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema indica que es una pirámide pentagonal con las siguientes medidas.

Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.

Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).

Y ahora el área de la base. Para ello en la fórmula general vamos  a sustituir por la fórmula para obtener el área de un pentágono regular, ya que la base es pentágono.  Es el área coloreada.

Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide pentagonal especificada.

Ahora obtenemos el volumen de la pirámide pentagonal  sustituyendo la fórmula del área de la base por la del área del pentágono y multiplicando por la altura del poliedro.

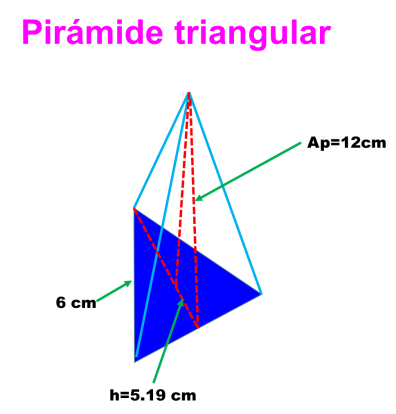
3.- Hallar el área total y el volumen de una pirámide regular triangular  cuyas medidas son las siguientes:

Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.

Recuerda que en una pirámide regular la altura de cada uno de los triángulos laterales (caras), llamada apotema del poliedro, es igual a la altura de la pirámide.

Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).

ÁREA SUPERFICIAL Y VOLUMEN DE UNA PIRABIME

Pirámide es un poliedro cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice común llamado vértice de la pirámide.

Recordemos  los elementos de una pirámide

Para calcular el área total de una pirámide es necesario conocer:

1. El área de la base (áb ), que es el polígono donde se apoya la pirámide.
2. El perímetro de la base(pb ), que es la longitud de todas las caras.
3. La apotema de la base (ap), que es la distancia del centro de la base a cualquier lado.
4. La apotema de la pirámide (Ap), que es la altura de una cara lateral.
5. La altura del poliedro (h), que es la distancia que hay del centro de la base al vértice de la pirámide.

Si deseas el formulario para obtener el volumen haz clic aquí

Las fórmulas generales para obtener el área y el volumen de una pirámide son las siguientes:

Ejemplos de ejercicios de área y volumen de una pirámide.

1.- Hallar el área total y el volumen de una pirámide cuadrangular cuya arista de la base mide 10, la altura de 12 cm y un Apotema del poliedro de 13 cm.

Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema

indica que es una pirámide cuadrangular con las siguientes medidas:

Obtengamos primero el área lateral (el de las cuatro caras triangulares) que es el área coloreada.

Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).

Y ahora el área de la base. Para ello en la fórmula general vamos  a sustituir por la fórmula para obtener el área de un cuadrado, ya que la base es cuadrangular.  Es el área coloreada.

Ver vídeo (Para recordar cómo se obtiene el área de un cuadrado).

Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide cuadrangular especificada.

Ahora obtenemos el volumen de la pirámide cuadrangular  sustituyendo la fórmula del área de la base por la del área del cuadrado y multiplicando por la altura del poliedro.

2.- Hallar el área total y el volumen de una pirámide regular pentagonal cuya altura mide 3.20m, el lado de la base 0.87185m, el apotema del poliedro 3.25576m;  y el apotema de la base 0.60m

Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema indica que es una pirámide pentagonal con las siguientes medidas.

Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.

Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).

Y ahora el área de la base. Para ello en la fórmula general vamos  a sustituir por la fórmula para obtener el área de un pentágono regular, ya que la base es pentágono.  Es el área coloreada.

Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide pentagonal especificada.

Ahora obtenemos el volumen de la pirámide pentagonal  sustituyendo la fórmula del área de la base por la del área del pentágono y multiplicando por la altura del poliedro.

3.- Hallar el área total y el volumen de una pirámide regular triangular  cuyas medidas son las siguientes:

Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.

Recuerda que en una pirámide regular la altura de cada uno de los triángulos laterales (caras), llamada apotema del poliedro, es igual a la altura de la pirámide.

Ver vídeo (Para recordar cómo se obtiene el área de un triángulo).

superación tercer periodo

Área y volumen de un prisma.

Para calcular el área total de un prisma siempre es necesario conocer tres medidas:

1. El área de una base.
2. El perímetro de la base
3. La altura del prisma

Las fórmulas generales para obtener el área y el volumen de cualquier prisma son las siguientes:

Formulario para obtener volumen de prismas. Haz clic aquí.

Resolvamos ejercicios de ejemplos específicos.

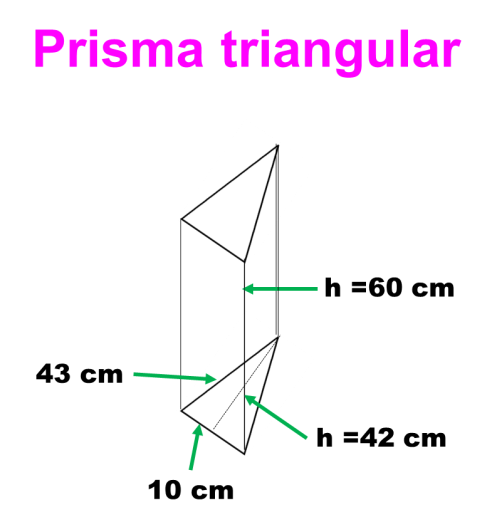
1.- Hallar el área total y el volumen de un prisma triangular cuya base mide 10 x 43 y con una altura de 42 cm; si la  altura el prisma mide 60 cm.

Nos enfocamos en la forma de las bases del prisma para despejar estas fórmulas. El problema indica que es un prisma triangular con las siguientes medidas.

Obtengamos primero el área lateral (el de las tres caras) que es el área coloreada.

Ver vídeo (para recordar cómo se obtiene el área de un rectángulo).

Y ahora el área de las bases. Para ello en la fórmula general vamos  a sustituir por la fórmula para obtener el área de un triángulo, ya que la base es triangular; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, triángulos isósceles). Es el área coloreada.

Ver vídeo (para recordar cómo se obtiene el área de un triángulo).

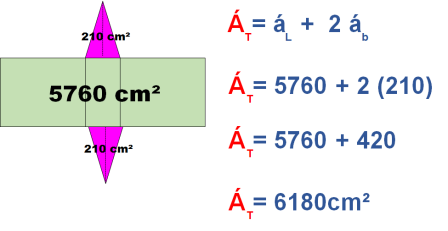
Por último sumaremos los valores del área lateral y del área de las dos basespara obtener el área total del prisma triangular especificado.

Ahora obtenemos el volumen del prisma triangular  sustituyendo la fórmula del área de la base por la del área del triángulo y multiplicando por la altura del poliedro.

2.- Hallar el área total y el volumen de un prisma cuadrangular regular cuyo lado de la base mide 1.20 m y la altura de 4 m.

Nos enfocamos en la forma de las bases del prisma para despejar estas fórmulas. El problema indica que es un prisma cuadrangular regular; que es el prisma que tiene como bases dos cuadrados y sus caras son cuatro rectángulos iguales.

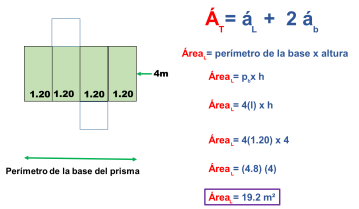
Obtengamos primero el área lateral (el de las cuatro caras rectangulares iguales) que es el área coloreada.

Ver vídeo (para recordar cómo se obtiene el área de un rectángulo).

Y ahora el área de las bases. Para ello en la fórmula general vamos  a sustituir por la fórmula para obtener el área de un cuadrado, ya que la base es cuadrangular; y después el resultado se multiplicará por 2 (ya que el prisma tiene dos bases iguales, en este caso, cuadrados). Es el área coloreada.

Ver vídeo (para recordar cómo se obtiene el área de un cuadrado).

Por último sumaremos los valores del área lateral y del área de las dos basespara obtener el área total del prisma cuadrangular regular especificado.

Ahora obtenemos el volumen del prisma cuadrangular regular  sustituyendo la fórmula del área de la base por la del área del cuadrado y multiplicando por la altura del poliedro.